2025年9月25日上午，信阳师范大学数学与统计学院尹佳斌副教授应邀为我院师生作了一场题为“闵可夫斯基空间中类空超曲面的稳定性与刚性结果”的学术报告。

报告介绍了通过使用带有P函数和积分恒等式的Weinberger型方法，建立了闵可夫斯基空间中类空超曲面的一些刚性定理。首先，对于可表示为图形式的类空超曲面M，若高阶平均曲率比为常数，且边界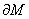位于一个与超曲面以固定角相交的超平面上，则该超曲面必为双曲抛物面的一部分。其次，对于边界位于一个双曲抛物面或光锥上的凸类空超曲面，若高阶平均曲率比为常数，且边界上超曲面与双曲抛物面（或光锥）的法向量之间的角函数为常数，则此类超曲面也必为双曲抛物面的一部分。

通过尹老师的报告，师生们学习了闵可夫斯基空间中类空超曲面的一些刚性定理，极大丰富了自身的知识，受益匪浅。报告结束后，参会师生就相关问题与尹老师进行了深入的讨论。

报告人简介：尹佳斌，信阳师范大学副教授，硕士生导师。研究方向聚焦于微分几何，主持国家自然科学基金两项，在AIM、CVPDE、SCM等期刊发表论文十余篇。